什麼是時間複雜度
執行次數隨資料量大小變化的趨勢。執行次數越多,表示演算法花費的時間越長,執行速度越慢。
常見時間複雜度由快至慢(資料量增長速度越快)為
1. 常數時間複雜度O(1),指無論資料量多少,執行次數固定。
2. 指數時間複雜度O(logn),資料量增加,執行次數增長緩慢。如原始資料量為8,採用指數時間複雜度,資料量與執行次數的關係式(資料量=執行次數)為log8=3次,增加8個資料,資料量與執行次數的關係式為log16=4次,所以增加8個資料,執行次數才會加1。
3. 線性時間複雜度O(n),資料量加1個,執行次數加1次。如原始資料量為8,採用線性時間複雜度,資料量與執行次數的關係式為8=8次,增加8個資料,資料量與執行次數的關係式為16=16次,所以增加8個資料,執行次數增加8次。
4. 線性對數時間複雜度O(nlogn),如原始資料量為8,採用線性對數時間複雜度,資料量與執行次數的關係式為8log8=24次,增加8個資料,資料量與執行次數的關係式為16log16=64次,所以增加8個資料,執行次數增加40次。
5. 平方函數時間複雜度O(n^2),如原始資料量為8,採用平方函數時間複雜度,資料量與執行次數的關係式為8^2=64次,增加8個資料,資料量與執行次數的關係式為16^2=256次,所以增加8個資料,執行次數增加192次。
給定一數列,算其中有多少個逆序對中的暴力求解時間複雜度就是O(n^2)。
6. 多項式函數時間複雜度O(n^k),如O(n^3)且原始資料量為8,採用多項式時間複雜度,資料量與執行次數的關係式為8^3=512次,增加8個資料,資料量與執行次數的關係式為16^3=4096次,所以增加8個資料,執行次數增加3584次。
7. 指數函數時間複雜度O(2^n),如原始資料量為8,採用多項式時間複雜度,資料量與執行次數的關係式為2^8=256次,增加8個資料,資料量與執行次數的關係式為2^16=65536次,所以增加8個資料,執行次數增加65280次。例如:費氏數列函數的遞迴式。
8. 階乘函數時間複雜度O(n!),如原始資料量為8,採用階乘函數時間複雜度,資料量與執行次數的關係式為8!=40320次,增加8個資料,資料量與執行次數的關係式為16!=一個很大的數,所以增加8個資料,執行次數增加很大的數次。
圖、常見時間複雜度執行次數比較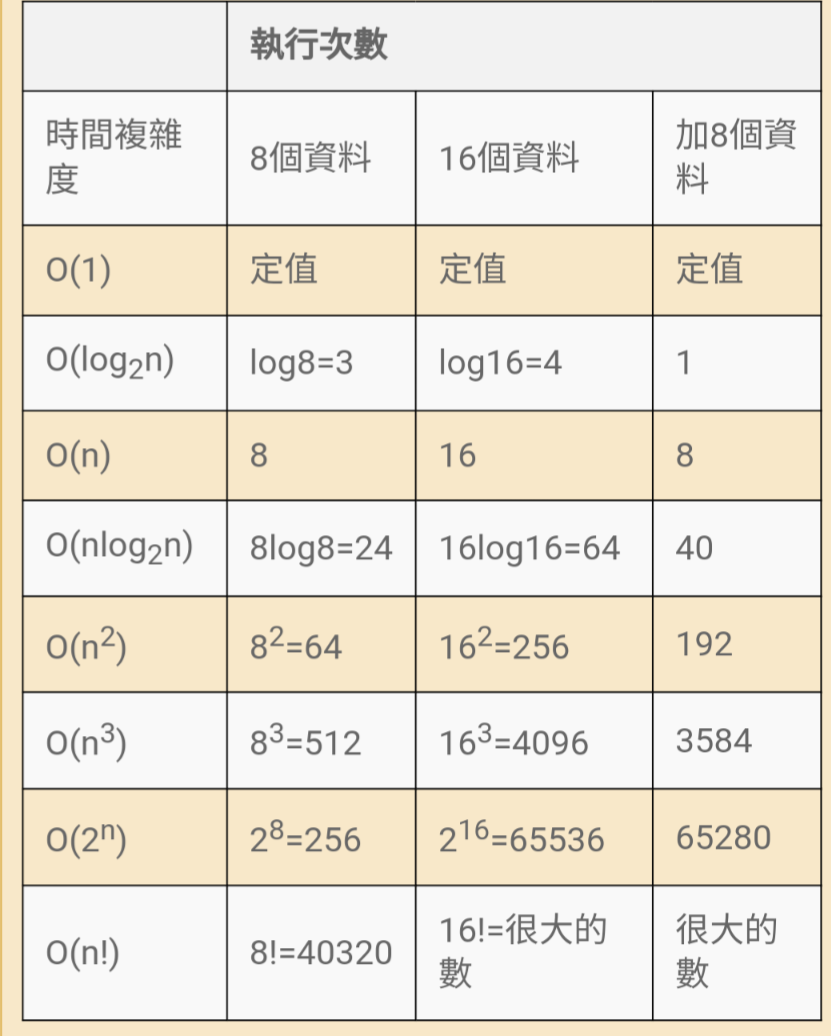
沒有留言:
張貼留言
寫下幸福點子吧!